Jak obliczyć efektywną roczną stopę procentową?

Z lekcji dowiesz się:

• Jak obliczyć zysk, przy kapitalizacji rzadszej niż rok?

• Ile zarobimy, przy odsetki kapitalizują się częściej?

• Co to jest efektywna stopa procentowa?

Zadanie 1

Efektywna Roczna Stopa Procentowa (odsetki kapitalizowane częściej niż raz na rok)

Kwota 10000 zł. Lokata 12 miesięczna, stopa procentowa 6% w stosunku rocznym.

Klasycznie zadanie zaczynamy od przygotowania tabelki z danymi (rys. 1).

(Rys. 1)

W pierwszej kolejności zastosujemy metodę obliczeniową. Widzimy, że liczbę okresów czyli n znamy z zadania, wiec pozostaje nam policzyć wartość naszego oprocentowania w stosunku rocznym, a także kwotę, która uzyskamy po roku lokaty.

Oprocentowanie w stosunku rocznym:

Oprocentowanie / liczba okresów (rys. 2).

(Rys. 2)

Następnie należy obliczyć końcową wartość lokaty. Skorzystamy w tym celu z dobrze znanej funkcji FV (rys. 3).

(Rys. 3)

Jako parametry wybieramy obliczoną w poprzednim kroku stopę procentową, liczbę okresów oraz kwotę początkową (należy pamiętać, za ta wartość musi być z minusem).

Po obliczeniu powyższych parametrów, możemy obliczy

roczną efektywną stopę procentową. W tym celu zastosujemy wzór i otrzymamy wartość efektywnej rocznej stopy procentowej.

Wartość końcowa lokaty – wartość początkowa lokaty/wartość początkowa lokaty (rys. 4).

(Rys. 4)

Drugim sposobem wykorzystywanym do obliczenia efektywnej rocznej stopy procentowej może być skorzystanie ze wzoru (rys. 5):

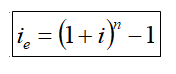
 (Rys. 5)

Możemy go opisać jako:

(1+ oprocentowanie)^liczba okresów -1 (rys. 6).

(Rys. 6)

W ostatnim kroku skorzystamy z funkcji efektywna

EFEKTYWNA(stopa_nominalna;okresy)

Argumenty funkcji:

Stopa_nominalna - Nominalna stopa procentowa.

Okresy - Liczba kapitalizacji w roku.

Postać funkcji to (rys. 7):

(Rys. 7)

Zadanie 2

Efektywna Roczna Stopa Procentowa (odsetki kapitalizowane rzadziej niż raz na rok).

W wyniku zainwestowania 100 tys. zł po 4 latach otrzymujemy 150 tys. zł. Naszym zadaniem jest obliczenie rocznej efektywnej stopy procentowej w oprocentowaniu: a) prostym, b) składanym, c) ciągłym.

Standardowo zaczynamy od przygotowania tabelki z danymi. W zadaniu nie mamy zmiennej opisującej oprocentowanie, dlatego należy policzyć ją stosując wzór:

Wartość końcowa lokaty – wartość początkowa lokaty/ wartość początkowa lokaty (rys. 8):

(Rys. 8)

Następnie wykorzystując podane wzory (rys. 9):

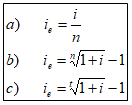
(Rys. 9)

Możemy obliczyć roczną efektywną stopę procentową w oprocentowaniu prostym:

Oprocentowanie/liczba okresów (rys. 10):

(Rys. 10)

Oraz składnym i ciągłym, gdzie stosujemy dokładnie taki sam wzór:

(1+ Oprocentowanie) ^ (1/liczba okresów) – 1 (rys. 11):

(Rys. 11)

Możemy także skorzystać z funkcji nominalna:

NOMINALNA(stopa_efektywna;okresy)

Argumenty funkcji:

Stopa_efektywna - Efektywna stopa procentowa.

Okresy - Liczba kapitalizacji w roku.

Funkcja ta ma postać (rys. 12):

(Rys. 12)

Wynik funkcji należy podzielić jeszcze przez 4, ponieważ w zadaniu liczyliśmy lokatę w okresie 4 lat, a założonym celem było uzyskanie rocznej efektywnej stopy procentowej.

Warto zawsze też sprawdzić, czy wyniki są prawidłowe. W tym celu stosując policzoną efektywną stopę procentową odtworzymy wartości lokaty i zweryfikujemy czy w ostatnim (4) roku otrzymamy wartość 150 tys. zł

W tym celu zastosujemy wzór:

Wartość początkowa lokaty * (1 + oprocentowanie) (rys. 13):

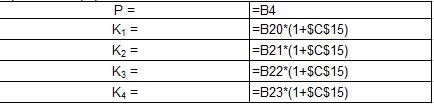
(Rys. 13)

Polecamy także:

• Jak obliczyć wartość: średnią, medianę i dominantę?

• Jak obliczyć kapitalizację odsetek?