Jak obliczyć kapitalizację odsetek?

Z lekcji dowiesz się:

• Po ilu latach ulokowana kwota osiągnie zakładaną wartość?

• Na czym polegają funkcje: NPER oraz RATE?

• Do czego służy pole „szacuj formułę”?

Zadanie 1

Po ilu latach rocznego oprocentowania w wysokości 5,75% kwota 200 tys. zł. osiągnie wartość 1 mln zł. w oprocentowaniu: a) prostym, b) składanym (kapitalizacja roczna) i c) ciągłym?

Tak jak w każdym zadaniu, powinniśmy zacząć od odpowiedniego zapisana danych, do których będziemy odwoływać się w trakcie wykonywania zadań.

Najpierw tworzymy tabelkę (rys. 1):

(Rys. 1)

I następnie zapisujemy wzory (rys. 2):

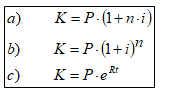
(Rys. 2)

Teraz możemy przejść do rozwiązywania pierwszego zadania:

• Oprocentowanie proste

Musimy przekształcić wszystkie wzory, ponieważ zależy nam aby obliczyć wartość n, czyli liczbę okresów.

Uzyskujemy następujące działanie:

(kwota końcowa – kwota początkowa)/(kwota początkowa * oprocentowanie) (rys. 3)

(Rys. 3)

• Oprocentowanie składane

Ponieważ n we wzorze występuje jako wartość potęgi, to do wyliczenia jej wartości niezbędne jest użycie funkcji logarytmu naturalnego (LN). Następnie po przekształceniu otrzymujemy następujące równanie:

LN(kwota końcowa/kwota początkowa)/(LN(1+wartość oprocentowania)) (rys. 4):

(Rys. 4)

Możemy również zastosować funkcje NPER (rys. 5):

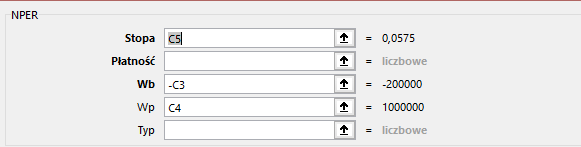
(Rys. 5)

W składni funkcji NPER występują następujące argumenty:

• Stopa – jest to argument wymagany, oznacza wysokość stopy procentowej obowiązującej podczas okresu trwania lokaty.

• Rata - argument wymagany, płatność dokonywana w każdym okresie, nie może się zmienić w czasie obowiązywania raty rocznej, w tym przypadku nie posiadamy tego argumentu, ponieważ w zadaniu nie ma informacji na temat kwoty jaka jest odkładana co miesiąc. Możemy go zastąpić argumentem Wp, aby funkcja działała poprawnie.

• Wb - argument wymagany, wartość początkowa lokaty, należy pamiętać aby wartość podawać jako liczbę ujemną.

• Wp - argument opcjonalny, przyszła (końcowa) wartość lokaty, argument wymagany w momencie pominięcia argumentu Rata.

• Typ - argument opcjonalny, jeżeli wartość obliczamy na koniec okresu, to należy nadać wartość 0 lub ją pominąć. W przypadku kiedy jest to początek okresu to argument przyjmuje wartość 1.

Ostateczna postać formuły (rys. 6):

(Rys. 6)

• Oprocentowanie ciągłe

Po przekształceniu otrzymujemy następujący wzór:

LN(kwota końcowa/kwota początkowa)/oprocentowanie (rys. 7):

(Rys. 7)

Zadanie 2

Ile powinno wynosić oprocentowanie lokaty 100 tys. zł, żeby po upływie 5 lat osiągnąć wartość 150 tys. zł w oprocentowaniu: prostym, składanym (kapitalizacja roczna) i ciągłym?

Podobnie jak w zadaniu pierwszym tworzymy tabele z danymi.

Przechodzimy do rozwiązania zadania. Skorzystamy z tych samych wzorów, jak w poprzednim zadaniu, z tym wyjątkiem, że teraz naszym zadaniem jest obliczenie oprocentowania. W tym celu musimy przekształcić wzory, tak aby niewiadomą było R=i.

• Oprocentowanie proste

Po przekształceniu otrzymujemy następujący wzór:

(kwota końcowa – kwota początkowa)/(kwota początkowa * liczba okresów) (rys. 8):

(Rys. 8)

• Oprocentowanie składane

Po przekształceniu otrzymujemy następujący wzór:

(kwota końcowa/kwota początkowa)^(1/liczba okresów) – 1 (rys. 9):

(rys. 9)

Pamiętamy, że w arkuszu kalkulacyjnym znak „^” oznacza potęgę.

W przypadku bardziej skomplikowanych działań, warto weryfikować ich sposób obliczenia wykorzystując jedną z opcji, jaką oferuje w swoim pakiecie Excel. Z zakładki Formuły, wybieramy pole szacuj formułę, w którym za pomocą przycisku „szacuj” można obserwować, jak krok po kroku obliczona została dana formuła (rys. 10 i 11).

(Rys. 10)

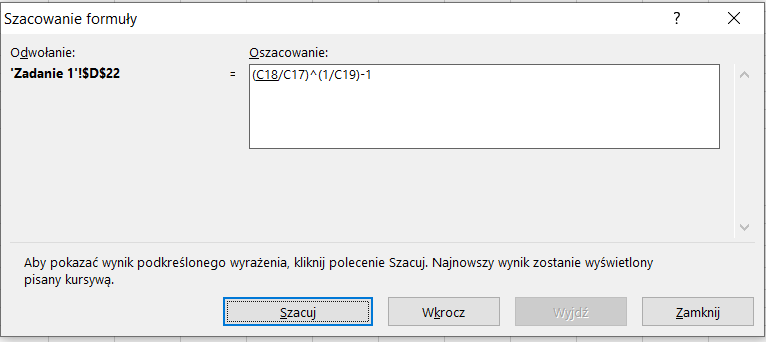
(Rys. 11)

Podobnie jak w 1 zadaniu, oprocentowanie składane można obliczyć za pomocą jednej z funkcji dostępnych w arkuszu kalkulacyjnym (rys. 12).

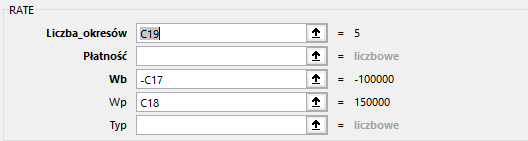
(Rys. 12)

W składni funkcji RATE występują następujące argumenty:

• Liczba_okresów - argument wymagany, jest to liczba wszystkich okresów podczas okresu spłaty.

• Rata - płatność dokonywana w każdym okresie, nie może się zmienić w czasie obowiązywania raty rocznej, w tym przypadku nie posiadamy tego argumentu, ponieważ w zadaniu nie ma informacji na temat kwoty, jaka jest odkładana co miesiąc, możemy go zastąpić argumentem Wp, aby funkcja działała poprawnie.

• Wb - argument wymagany, wartość początkowa lokaty, należy pamiętać aby wartość podawać jako liczbę ujemną.

• Wp - argument opcjonalny, przyszła (końcowa) wartość lokaty, argument wymagany w momencie pominięcia argumentu Rata.

• Typ - argument opcjonalny, jeżeli wartość obliczamy na koniec okresu, to należy nadać wartość 0 lub ją pominąć, w przypadku kiedy jest to początek okresu to argument przyjmuje jakąś wartość.

Ostateczna postać formuły (rys. 13):

(Rys. 13)

• Oprocentowanie ciągłe

Po przekształceniu otrzymujemy wzór:

LN(kwota końcową/kwota początkową)/liczba okresów (rys. 14):

(Rys. 14)

Polecamy także:

• Jak wyliczyć oprocentowanie zmienne?

• Jak obliczyć oprocentowanie: proste, składane i ciągłe?