Jak obliczyć oprocentowanie: proste, składane i ciągłe?

Z lekcji dowiesz się:

• Jak obliczyć wartość lokaty z różnym oprocentowaniem?

• Co to jest liczba Eulera, będąca podstawą logarytmu naturalnego?

• Przy jakich poleceniach używać funkcji FV?

Zadanie 1

Pierwsze, bardzo krótkie zadanie w którym policzymy wartość Liczby Eulera (Liczba E), która jest podstawą logarytmu naturalnego i będzie niezbędna do wykonania części zadania 2. Liczba E przyda się niejednokrotnie podczas pracy z Excelem.W przybliżeniu wynosi ona 2,718281828459.

Do jej wyliczenia wystarczy wpisać prostą formułę:

EXP(liczba), gdzie jako liczbę wpisuje podstawę logarytmu. W tym przypadku podstawa to po prostu liczba 1

EXP(1) – formuła, oblicza wartość Liczby Eulera w arkuszu kalkulacyjnym.

Zadanie 2

Treść zadania:

Obliczyć wartość lokaty 30 tys. zł po upływie 5 lat, przy rocznej stopie procentowej wynoszącej 6% (kapitalizacja roczna), w oprocentowaniu:

• Prostym

• Składanym (kapitalizacja ciągła)

• Ciągłym

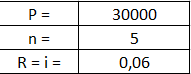
Dane do naszego zadania (rys. 1):

(Rys. 1)

Gdzie :

P = wartość początkowa

N = liczba okresów

I = oprocentowanie

Oprocentowanie proste

W pierwszym podpunkcie obliczymy wartość lokaty stosując oprocentowanie proste. Wykonamy obliczenia na dwa sposoby, stosując bezpośredni wzór, a także dłuższa metodę pośrednią obliczeniową.

Metoda obliczeniowa – Jako P podajemy wartość początkową naszej lokaty. Następnie wyliczamy oprocentowanie w każdym z 5 okresów. Jako, że jest to oprocentowanie proste, nie zmienia się ono wraz ze zmianą okresu. Formuła w każdym okresie wygląda tak samo, dlatego do jej wyliczenia należy zablokować komórki stosując znany już znak $,a następnie przeciągnąć w prawo. Żeby policzyć ile zarabiamy przy zadanym oprocentowaniu, należy zawsze wartość początkową policzyć przez to oprocentowanie (rys. 2).

(Rys. 2)

Po obliczeniu składowych z 5 okresów, następnie sumujemy je wraz z wartością początkową i uzyskujemy oczekiwany wynik (rys. 3).

(Rys. 3)

Dla sprawdzenia poprawności wyniku, policzmy jeszcze oprocentowanie za pomocą wzoru (rys. 4).

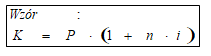
(Rys. 4)

Analogicznie do tabelki z danymi, którą wypisaliśmy na samym początku zadania, po prostu podstawiamy do wzoru (rys. 5).

(Rys. 5)

Wyniki się pokrywają więc możemy uznać ze zadanie zostało rozwiązane poprawnie.

Oprocentowanie składane:

Zadanie rozwiążemy korzystając aż z 3 sposobów. Podobnie jak w zadaniu poprzednim do opcji obliczeniowej i wzoru, pokażemy jedną z funkcji dostępnych w arkuszu kalkulacyjnym.

Zaczynamy od opcji obliczeniowej (rys. 6).

(Rys. 6)

Można zauważyć, że metoda obliczeniowa jest stosunkowo podobna do tej używanej w oprocentowaniu prostym, z ta różnicą, że jak sama nazwa wskazuje oprocentowanie mnożymy przez to, co udało nam się już odłożyć na lokacie. W tym celu stale powiększamy zakres sumy, która z każdym okresem wzrasta o wartość odłożoną w danym okresie.

Następnie, jak łatwo się domyślić sumujemy wszystkie wartości, nie zapominając o początkowej, w ten sposób otrzymujemy końcowy rezultat (rys. 7).

(Rys. 7)

Teraz to samo oprocentowanie policzymy używając wzoru (rys. 8).

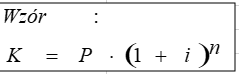
(Rys. 8)

Jeśli znamy znaczenie symboli, użytych we wzorze, zadanie oczywiście jest bardzo proste. Znowu należy podstawić do wzoru wartości, jedyną trudnością może być potęga, która znajduje się we wzorze. Aby podnieść dowolną wartość do potęgi w arkuszu kalkulacyjnym należy użyć znaku ^ i wprowadzić po nim wartość potęgi (rys. 9).

(Rys. 9)

Analogicznie możemy użyć wzoru stosując formułę obliczeniowa, z jedyną różnicą że tu zwiększamy wartość potęgi wraz ze wzrostem okresu (rys. 10).

(Rys. 10)

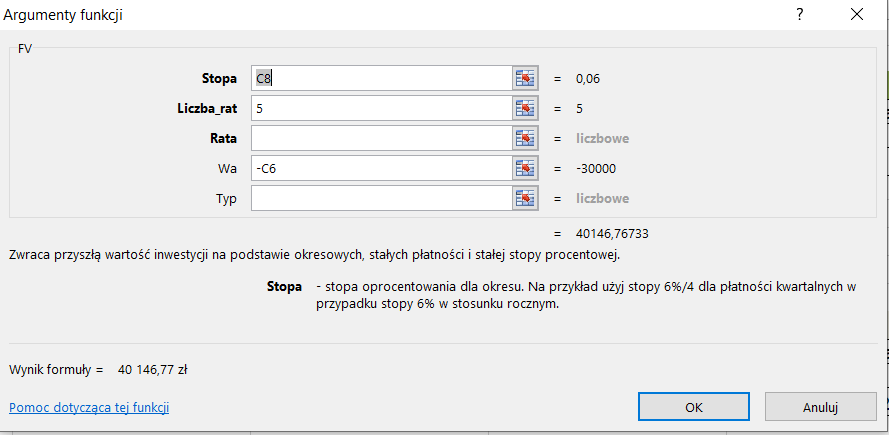
W ostatniej metodzie wykorzystamy funkcję FV, dostępną w arkuszu kalkulacyjnym (rys. 11).

(Rys. 11)

Funkcja nie jest trudna, przejdźmy więc po kolei:

Stopa - tutaj wprowadzamy wartość procentową lokaty.

Liczba rat – liczba okresów kapitalizacji lokaty.

Rata – tutaj przyjmuje wartość 0, ewentualnie zostawiamy pustą komórkę, obie wersje są tożsame.

Wa – czyli wartość początkowa, ważne abyśmy pamiętali o dodaniu znaku minus przed wprowadzoną wartością w przeciwnym razie wynik wyjdzie na minusie.

Typ – nie wprowadzamy żadnej wartości.

W przypadku obliczenia wartości FV w każdym okresie postępujemy analogicznie jak w poprzednich przykładach (rys. 12).

(Rys. 12)

Oprocentowanie ciągłe

W przypadku oprocentowania ciągłego skorzystamy ze wzoru. Niezbędna będzie znajomość obliczania liczby E, poznanej w zadaniu 1 (rys. 13).

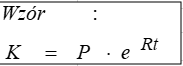
(Rys. 13)

Zgodnie ze wzorem, podstawiamy wartości (rys. 14).

(Rys. 14)

Wartość exp, wyliczamy tak samo jak w zadaniu 1 z tą różnicą że tu podstawą jest iloczyn oprocentowania i liczby okresów podanych w treści zadania.

Podobnie jak w poprzednich przykładach możemy wyliczyć wartość licząc po kolei każdy okres (rys. 15).

(Rys. 15).

Liczba e zwana też liczbą Eulera oraz liczbą Napiera (Nepera) jest jedną z najważniejszych stałych matematycznych. Znamy ją przede wszystkim jako podstawę logarytmu naturalnego. Występuje tam, gdzie mamy do czynienia ze wzrostem (np. w finansach, dynamice populacji czy zagadnieniach fizycznych). Jest to liczba niewymierna o rozwinięciu dziesiętnym nieskończonym nieokresowym - jej wszystkich cyfr po przecinku nie poznamy nigdy. Jej wartość w przybliżeniu to: 2,718 281 828 459 045 235 36.

Polecamy także:

• Ile wynosi roczna stopa procentowa kredytu?

• Jak wygenerować zaproszenie na konferencję?