Jak obliczyć rzeczywistą stopę procentową uwzględniając inflację?

Z lekcji dowiesz się:

• Jak wyliczyć realną wartość odsetek z lokaty bankowej?

• O tym, że inflacja to podstawowy wskaźnik w matematyce finansowej!

• Kiedy faktycznie rośnie kapitał!

Inflacja to proces przeciętnego wzrostu cen w gospodarce, naszym zadaniem będzie obliczenie stopy inflacji oraz zysku z lokaty uwzględniającego jej poziomu.

Zadanie 1

Obliczamy czynniki inflacji 1+iinf względem poprzedniego miesiąca.

Z tabelki z wyliczonymi stopami inflacji pobieramy wartość odpowiadającą właściwej dacie np. (styczeń 2010) i dodajemy 1, dokładnie tak samo jak jest we wzorze: 1+iinf. W komórce otrzymujemy następująca wartość (rys. 1):

(Rys. 1)

Przeciągamy wartość formuły w prawo oraz do dołu i otrzymujemy (rys. 2):

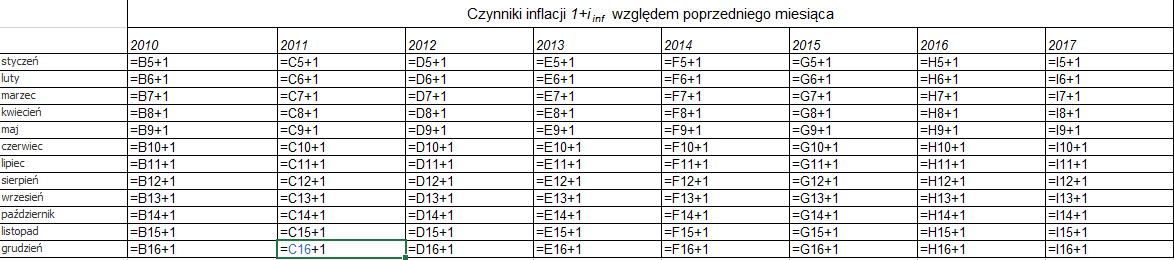
(Rys. 2)

Zadanie 2

Obliczamy stopę inflacji względem grudnia roku poprzedniego.

W tym celu stosujemy prosty wzór czyli iloczyn czynnika inflacji z każdego następnego miesiąca i odejmujemy od otrzymanej wartości 1, ponieważ stopy inflacji przedstawiamy w postaci procentowej. Aby moc swobodnie przesuwać formułę w prawo i w dół należy zablokować numer wiersza w pierwszym argumencie funkcji iloczyn (rys. 3).

(Rys. 3)

Otrzymujemy następujące wartości formuły w całej tabeli (rys. 4).

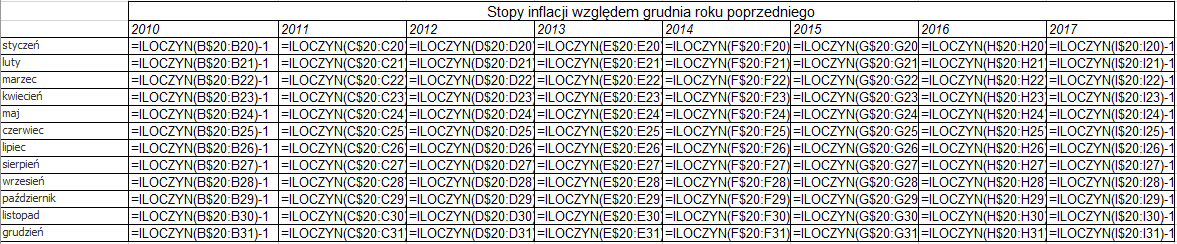
(Rys. 4)

Zadanie 3

Obliczamy rzeczywistą stopę procentową, jeśli roczna stopa procentowa w banku wynosi 10%, zaś roczna stopa inflacji jest równa 5%.

Rozpoczynamy od przygotowania tabelki z danymi, które następnie użyjemy we wzorze (rys. 5).

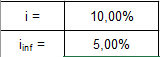
(Rys. 5)

Naszym zadaniem, jest policzenie wartości Ir dlatego należy przekształcić wzór, przez co otrzymamy następującą jego postać (rys. 6).

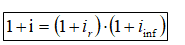
(Rys. 6)

Ir = 1+ stopa procentowa/ 1+ stopa inflacji -1 (Rys. 7).

(Rys. 7)

Zadanie 4

Obliczamy nominalną i realną wartość rocznej lokaty bankowej 50.000 zł oraz nominalną i realną wartość odsetek na koniec roku, jeżeli nominalna roczna stopa procentowa wynosi 7,55%, a stopa inflacji w tym roku wyniosła 1,6% (śródroczna stopa inflacji za 2018 rok).

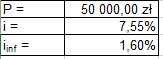
(Rys. 8)

Po przygotowaniu tabelki z danymi (rys. 8) należy policzyć nominalną wartość kapitału oraz nominalna wartość odsetek.

Nominalna wartość kapitału = wartość początkowa lokaty * (1+ nominalna roczna stopa procentowa) (rys. 9).

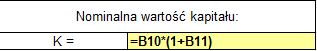
(Rys. 9)

Nominalna wartość odsetek = Nominalna wartość kapitału - wartość początkowa lokaty (rys. 9a).

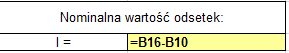
(Rys. 9a)

Do policzenia realnej wartości kapitału skorzystamy ze wzoru (rys. 10):

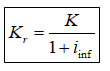
(Rys. 10)

Realna wartość kapitału = Nominalna wartość kapitału/ (1+ stopa inflacji) (rys. 11).

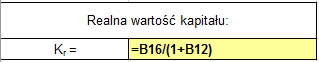
(Rys. 11)

Do policzenia realnej wartości odsetek skorzystamy ze wzoru (rys. 12):

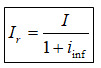
(Rys. 12)

Realna wartość odsetek = nominalna wartość odsetek/(1+stopa inflacji) (rys. 13).

(Rys. 13)

Na koniec podsumujemy wszystko w tabeli (rys. 14) i obliczymy:

Realny przyrost kapitału = realna wartość kapitału – wartość początkowa lokaty

Różnica = realna wartość odsetek – realny przyrost kapitału

(Rys. 14)

Na końcu sprawdzimy poprawność wyników:

Realna wartość kapitału = wartość początkowa lokaty – policzona różnica * (1+ nominalna roczna stopa procentowa) (rys. 15).

(Rys. 15).

Polecamy także:

• Jak obliczyć efektywną roczną stopę procentową?

• Jak obliczyć kapitalizację odsetek?