Tworzenie rankingów i zestawień za pomocą funkcji Pozycja

Z lekcji dowiesz się:

• Jak w sprytny sposób tworzyć rankingi i zestawienia?

• Co to jest „korelacja”? Jak działa?

• Przy jakich zadaniach używać funkcji Pozycja?

W bazie danych znajdują się wyniki zawodników w konkursie sportowym, a także ich parametry dotyczące wzrostu i wagi. Pierwszy problem, który napotykamy to zupełnie inne miary porównywanych wskaźników. Wzrost wyrażony w centymetrach, a waga w kilogramach. Błędem byłoby dodanie do siebie tych dwóch parametrów, dlatego zbudujemy za pomocą funkcji Pozycja ranking, który określi nam, którego z zawodników możemy uznać za najwyższego i najsilniejszego.

Omówmy w pierwszej kolejności funkcję Pozycja.

POZYCJA(liczba;lista;[lp])

Liczba - liczba, której pozycja ma zostać określona, wartości tej nie blokujemy,

Lista - tablica danych, z których ma zostać utworzony ranking. Zakres powinien zostać zablokowany, w ten sposób przeciągając funkcje do dołu, rozmiar listy pozostanie niezmieniony.

Lp - argument określający w jakiś sposób zamierzamy uszeregować wartości:

Zaczynamy od ustalenia rankingu zawodników pod kątem ich wzrostu. Wybieramy funkcję Pozycja i jako liczbę wskazujemy pierwszą wartość komórki z listy (wzrost pierwszego zawodnika) pamiętając, że nie blokujemy wartości tej komórki. Zakres tablicy, to wzrost wszystkich zawodników i tutaj te wartości blokujemy, ponieważ przesuwając formułę do dołu, chcemy żeby zmieniała się jedynie porównywana liczba, a nie zakres tablicy. Chcemy szeregować wartości rosnąco, dlatego wybieramy 1 i przeciągamy tak napisaną formule w obrębie tablicy (rys. 1).

(Rys. 1)

Dokładnie tak samo postępujemy budując ranking w przypadku wagi zawodników (rys. 2).

(Rys. 2)

Nieprzypadkowo, tworzyliśmy ranking szeregując wartości w sposób rosnący. Dzięki temu udało się stworzyć swoisty ranking punktowy, który dla osoby najwyższej lub najsilniejszej przypisał największą liczbę punktów (w tym przypadku pozycję). Pozwala to na zsumowanie dwóch rankingów, pomimo różnej skali porównywanych czynników (rys. 3).

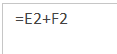
(Rys. 3)

Największa ilość punktów świadczy o największej sile (umownie uznajemy wzrost i wagę za definicję siły) danego zawodnika (rys. 4).

(Rys. 4)

Teraz ponownie stworzymy ranking zgodnie z metodyką jak przyjęliśmy we wcześniejszych punktach.

Zawodnik o największej liczbie punktów, zajmie „ostatnie” czyli 30 miejsce, które w tym przypadku jest najlepsze, ponieważ zajmowaną pozycję zamieniamy na punkty.

Kiedy mam już pełne zestawienie pozycji każdego zawodnika, policzymy współczynnik korelacji, między liczbą punktów, które uzyskał w zawodach, a liczbą punktów jakie uzyskał w naszym rankingu predyspozycji fizycznej. Sprawdźmy - czy siła wpływa na lepszy wynik zawodnika?

Korelacja – jest badaniem polegającym na sprawdzeniu czy dwie zmienne są ze sobą powiązane i wpływają na siebie wzajemnie. Inaczej mówiąc jak wzrost lub spadek jednej zmiennej wpływa na wartość drugiej. Prostym przykładem może być badanie korelacji między wzrostem metrażu mieszkania, a jego ceną. Łatwo się domyślić, że czym większy metraż, tym droższa nieruchomość. Możemy wtedy powiedzieć o korelacji dodatniej, czyli sytuacji, w której wzrost lub spadek jednej zmiennej powoduje analogiczną reakcję drugiej. Korelacja ujemna to oczywiście sytuacja odwrotna od opisywanej, np. im niższa cena produktu tym większa jego sprzedaż. W tym przypadku wzrost lub spadek zmiennej powoduje spadek lub wzrost drugiej zmiennej.

Ważne, aby pamiętać że wartość współczynnika korelacji jest zawarta w przedziale <-1,1> Jeżeli współczynnik, wyjdzie poza ten przedział należy sprawdzić, czy nie popełniliśmy błędu.

W zależności od wartości współczynnika wyróżnia się korelacje:

• <-1, -0,5> silna korelacja ujemna

• <-0,5, -0,3> umiarkowana korelacja ujemna

• <-0,3, 0> słaba korelacja ujemna

• <0, 0,3> słaba korelacja dodatnia

• <0,3, 0,5> umiarkowana korelacja dodatnia

• <0,5, 1> silna korelacja dodatnia

Tyle teorii, przejdźmy zatem do praktyki. Aby policzyć współczynnik korelacji skorzystamy z tożsamej nazwy funkcji dostępnej w arkuszu kalkulacyjnym. Jej budowa jest bardzo prosta. Wybieramy dwa zakresy komórek (tablic), które chcemy ze sobą porównać obliczając współczynnik korelacji. Nie musimy nic blokowa

, ani przeciągać, wynik otrzymujemy w jednej komórce.

Obliczymy współczynnik korelacji między rankingiem zawodników, a ich sumą punktów w zawodach sportowych. Sprawdzimy czy siła mierzona wzrostem i wagą przekłada się na końcowy wynik.

Wartość współczynnika korelacji wynosi -0,27 czyli istnieje słaba korelacja ujemna. Można uznać, że siła nie wpływa w znaczny sposób na ilość punktów, a jeśli już taki związek istnieje, to działa w sposób odwrotny. Widzimy zatem, że to ile mamy wzrostu i ile ważymy, w tym przypadku nie wpływa na naszą sprawność sportową (rys. 5).

(Rys. 5)

Dla przetestowania współczynnika korelacji zbudujemy dwie tablice (rys. 6):

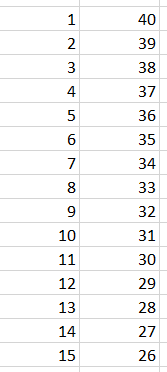
(Rys. 6)

Zastosujemy w nich współczynnik korelacji analogicznie jak wcześniej (rys. 7):

(Rys. 7)

Jak łatwo się domyślić, wynik to -1. Mamy idealną korelację ujemną czyli wzrost jednej zmiennej wpływa na spadek zmiennej drugiej, co łatwo zauważyć na przygotowanym zestawie danych.

Polecamy także:

• Zabezpieczenia w arkuszu kalkulacyjnym!

• Wykorzystanie połączonych formuł: index oraz podaj pozycję!