Ile mieszanek bakaliowych po 100 gr. wyprodukujesz z kontenera: rodzynek i orzechów i migdałów? Solver to wyliczy!
Solver jest jednym z dodatków umożliwiających lepszą analizę danych dostępnych w arkuszu kalkulacyjnym. Dzięki niemu można ustalić maksymalną lub minimalną wartość określonej komórki (komórka celu) przez zmianę innych komórek (komórki decyzyjne), które mogą podlegać pewnym ograniczeniom. Dodatek Solver jest stosowany do ustalenia: optymalnych cen, maksymalizacji przychodu, minimalizacji kosztów produkcji, a także do ustalania budżetów.
Z lekcji dowiesz się:
-
Przy jakich działaniach biznesowych sprawdzi się Solver?
-
Po co szukać optymalnych wartości?
-
Jaką kombinacją liczb lub danych (np. wagowych) uzyskać założoną wartość?
Z lekcji dowiesz się:
-
Przy jakich działaniach biznesowych sprawdzi się Solver?
-
Po co szukać optymalnych wartości?
-
Jaką kombinacją liczb lub danych (np. wagowych) uzyskać założoną wartość?
Rozwiążemy dwa zadania, które przybliżą nam możliwości, które daje Solver i pozwolą lepiej zrozumieć budowę i wykorzystanie tego niezwykle ciekawego dodatku w arkuszu kalkulacyjnym.
Zadanie 1
W kolumnie C widocznym na filmiku znajdują się losowo wybrane liczby. Naszym zadaniem jest ustalić za pomocą Solvera, która kombinacja liczb da w sumie wartość 230 (jest to oczywiście wartość przykładowa).
W kolumnie D umieszczamy losowo wybrane wartości 0 i 1.
W kolumnie F2, umieszczamy komórkę celu, która będzie wynikiem naszego Solvera (w tym przypadku będzie to wartość 230) i wpisujemy tam formułę (rys. 1).
![]()
(Rys. 1)
W ten sposób Solver trafnie rozpozna, które wartości należy zsumować i przy tych wartościach w kolumnie D przypisze wartość 1.
Kiedy mamy już niezbędne dane, można przygotować Solvera.
Wybieramy zakładkę Dane i z prawej strony wybieramy Solver (rys. 2).

(Rys. 2)
Jeśli nie posiadamy zainstalowanego dodatku, to wybieramy Opcje, następnie przechodzimy do sekcji dodatki. Wybieramy Dodatki programu Excel i klikamy przejdź (rys. 3).
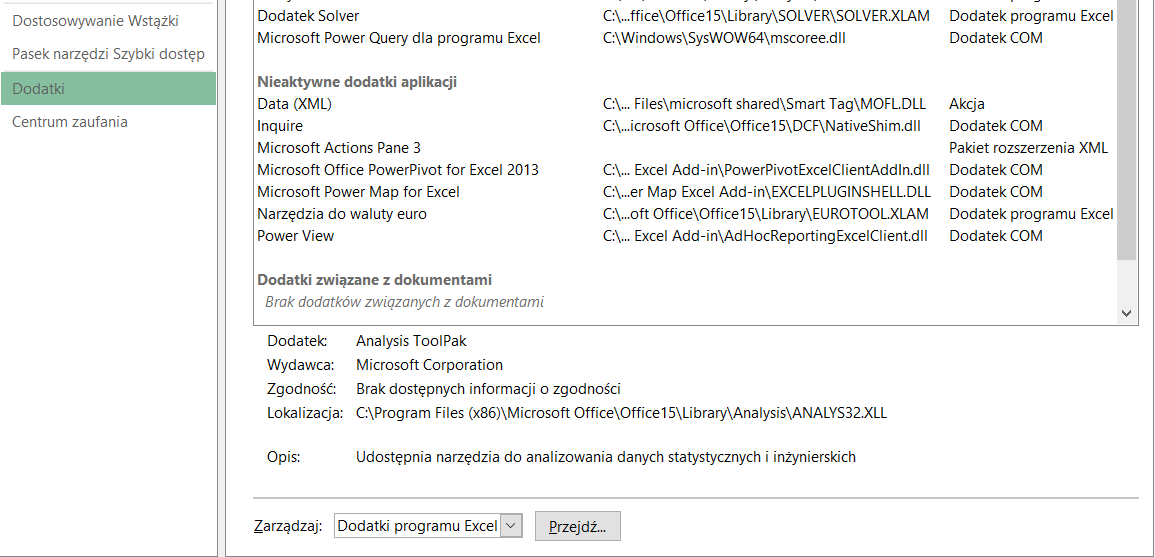
(Rys. 3)
Następnie wystarczy tylko zaznaczyć Dodatek Solver i gotowe (rys. 4).
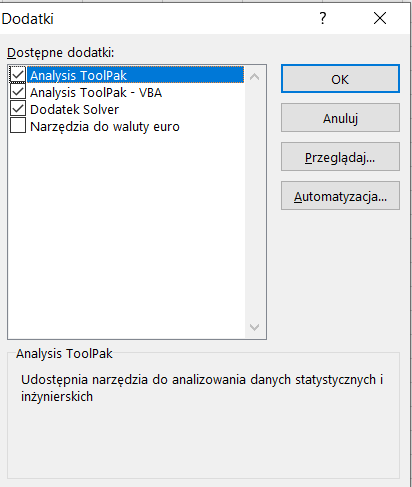
(Rys. 4)
Po pomyślnym zainstalowaniu dodatku, klikamy Solver i pojawia się okno dialogowe, które należy odpowiednio uzupełnić.
Zaczynamy od ustalenia komórki celu, czyli F2 (rys. 5).

(Rys. 5)
Ponieważ zależy nam na konkretnej wartości (230) to klikamy wartość i podajemy, jaka dokładnie nas interesuje (rys. 6).
![]()
(Rys. 6)
Komórki decyzyjne, to kolumna D, w której umieściliśmy 0 i 1, niezbędne do identyfikacji odpowiednich liczb (rys. 7).
![]()
(rys. 7)
Nie mamy w tym zadaniu, żadnych ograniczeń, ale aby dodatek poprawnie rozpoznał komórki decyzyjne należy ustawić je jako wartości binarne, czyli przyjmujące wartości 0 lub 1 (rys. 8)

(Rys. 8)
Po uzupełnieniu wszystkich parametrów klikamy Rozwiąż (rys. 9).
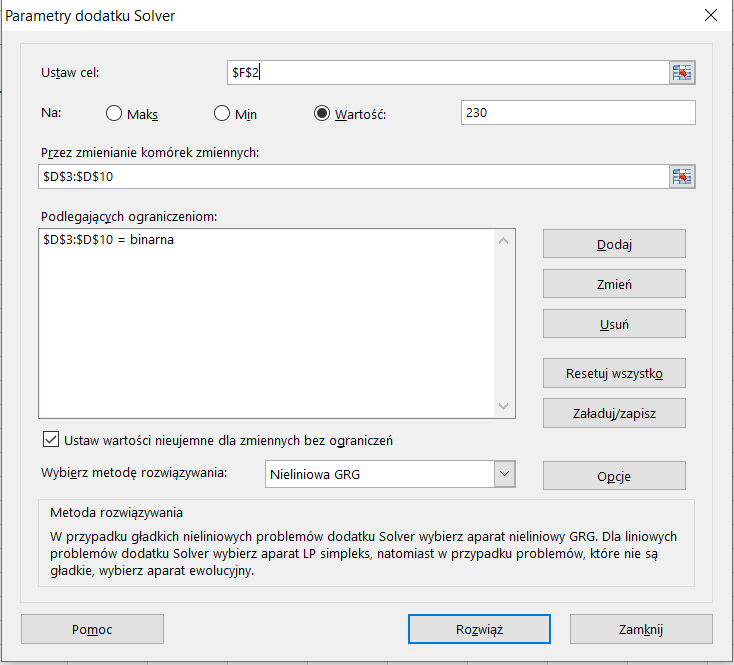
(Rys. 9)
Zadanie 2
Treść zadania:
Firma Bakaluś importuje bakalie, które pakuje w opakowania po 100 gram i sprzedaje sieciom handlowym w postaci mieszanek bakaliowych. Mieszanka „Bakaliowy Frykas” zawiera 30% orzechów ziemnych, 10% orzechów laskowych, 10% orzechów nerkowca, 10% migdałów i 40% rodzynek. Mieszanka „Orzechowy Przysmak” zawiera 40% orzechów laskowych, 40% orzechów nerkowca oraz 20%migdałów. Mieszanka „Ziemniaczek” zawiera wyłącznie orzechy ziemne. Mieszanka „Studencka” zawiera 20% orzechów nerkowca, 40% migdałów i 40% rodzynek. Firma dostała przydział na zakup:
-
400 kg orzechów ziemnych,
-
90 kg orzechów laskowych,
-
102 kg orzechów nerkowca,
-
105 kg migdałów,
-
285 kg rodzynek.
Ceny sprzedawanych mieszanek wynoszą za jedno opakowanie wynoszą:
-
„Bakaliowy Frykas” - 6,80 zł,
-
„Orzechowy Przysmak” - 8,60 zł,
-
„Ziemniaczek” - 4,60 zł,
-
„Studencka” - 8,00 zł.
Naszym zadaniem jest ustalić miesięczny plan produkcji firmy Bakaluś maksymalizujący przychód ze sprzedaży mieszanek bakaliowych.
W tym celu tworzymy tabelkę z danymi, która ułatwi późniejsze przeniesienie danych do Solvera (rys. 10).
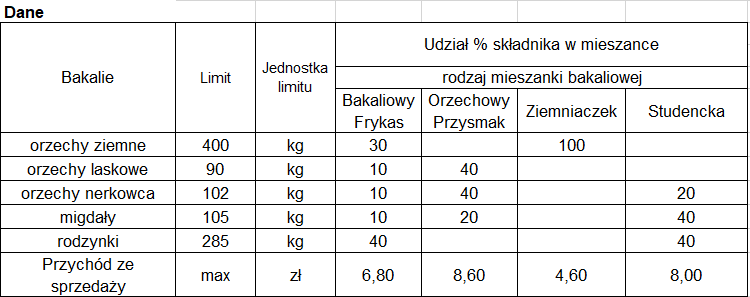
(Rys. 10)
Uwaga: ilość poszczególnych bakalii w mieszankach jest podana w kilogramach, natomiast z zadania wiemy, że pojedyncze opakowanie ma pojemność 100g. Należy zatem podzielić wartości przez 100 i tak przygotowane dane skopiować do tabelki, którą użyjemy bezpośrednio do Solvera.
Przechodzimy do drugiej zakładki, gdzie znajduje się wzór tabeli (rys. 11).
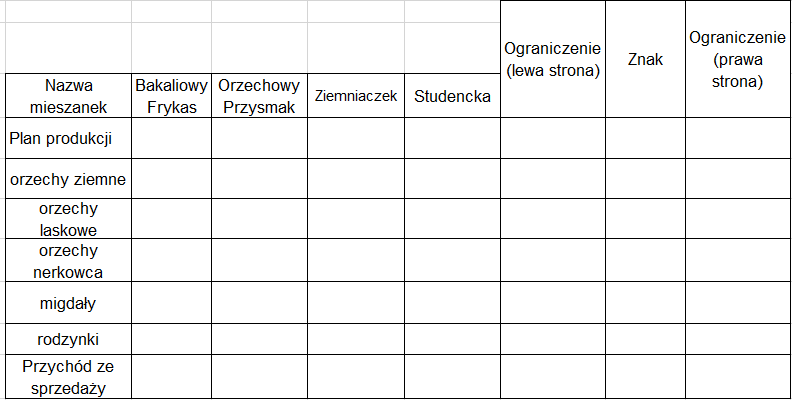
(Rys. 11)
W wierszu Plan produkcji wpisujemy losowe wartości, ponieważ w ich miejscu Solver wygeneruje optymalne wartości (podobnie jak to miało miejsce w przypadku 0 i 1 w zadaniu 1).
Następnie wartości w wierszach dotyczących składu poszczególnych bakalii, a także przychodu ze sprzedaży, kopiujemy z wcześniej przygotowanych wartości (rys. 12).
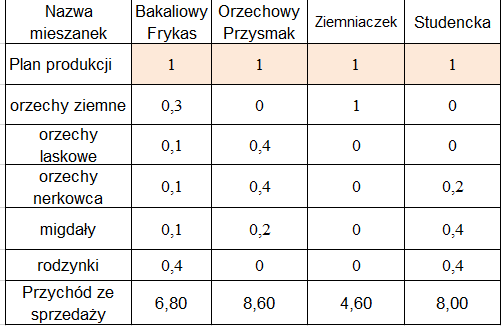
(Rys. 12)
W kolumnie - Ograniczenie prawa strona - wprowadzamy limity dotyczące zakupu poszczególnych składników (rys. 13).
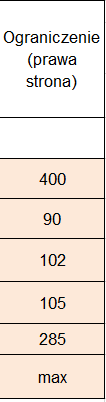
(Rys. 13)
W kolumnie - Ograniczenie lewa strona - ponownie wykorzystamy niezbędną przy pracy z Solverem funkcje suma iloczynów, która pokazana została w poprzednim zadaniu (Rys. 14).
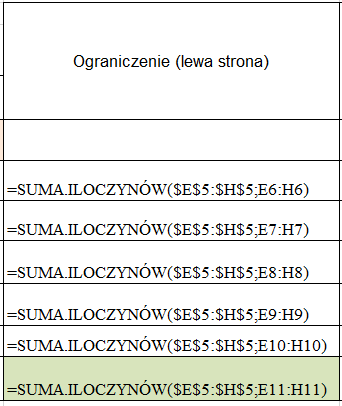
(Rys. 14)
W kolumnie - Znak - wybieramy odpowiedni znak determinujący ograniczenie. W tym przypadku jest to bardzo prost,e wszystkie ograniczenia z lewej strony muszą być mniejsze lub równe od ograniczeń z prawej strony (rys. 15).
![]()
(Rys. 15)
Gdy tabelka jest uzupełniona, można przystąpić do szukania optymalnego rozwiązania za pomocą Solvera.
Jako funkcje celu wyznaczamy komórkę, która określi maksymalny możliwy przychód, który można uzyskać (rys. 16).

(Rys. 16)
Jako, że nie jest szukana tutaj konkretna wartość, to wybieramy aby rozwiązanie Solver znalazło wartość Maks. Analogicznie, w przypadku poszukiwania np. minimalnych kosztów produkcji - należałoby wybrać Min. (rys. 17).
![]()
(Rys. 17)
Komórkami decyzyjnymi są - ilości opakowań jakie należy wyprodukować aby osiągnąć maksymalny przychód (rys. 18).

(Rys. 18)
Na koniec należy uwzględnić ograniczenia wynikające z parametrów produkcji. Wynika to z zasady, że lewa strona ograniczenia musi być mniejsza lub równa prawej stronie ograniczenia (rys. 19).
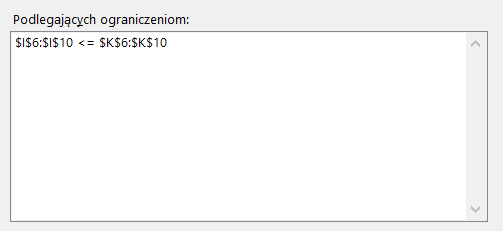
(Rys. 19)
Po uzupełnieniu wszystkich parametrów klikamy Rozwiąż i otrzymujemy rozwiązanie (rys. 20)
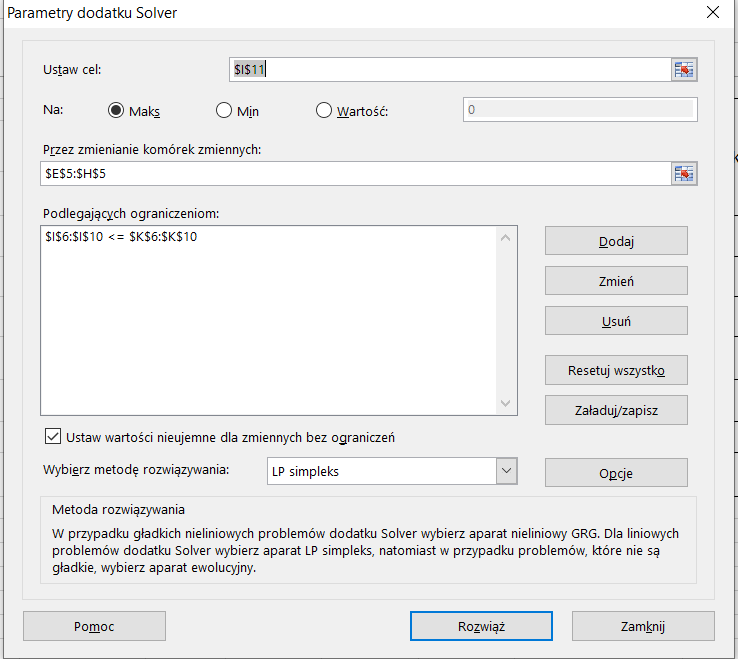
(Rys. 20)
Solver wygenerował wartości odpowiednie dla planu produkcji każdej z mieszanek. Dla sprawdzenia należy zweryfikować, czy żadne ograniczenia nie pokrywają się na siebie. W zadaniu widzimy, że wszystko zostało wykonane poprawnie i otrzymaliśmy optymalne poziom produkcji mieszanek bakaliowych (rys. 21).
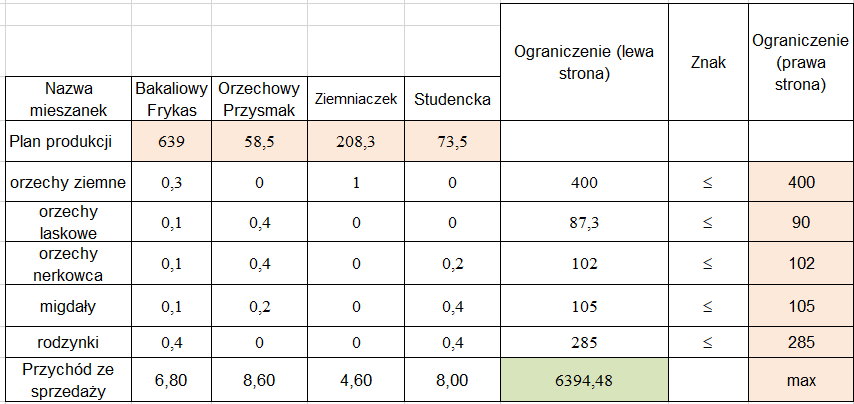
(Rys. 21)
Wskazane przykłady - to oczywiście jedynie mała cześć problemów, które można rozwiązać przy pomocy dodatku Solver. Zachęcamy do przenalizowania materiału, filmiku i poćwiczenia tych zadań samodzielnie, a także dalszego poszerzania wiedzy w zakresie tego dodatku.
Polecamy także:
Jeszcze się wahasz?
Zobacz, co zyskasz, mając pełny dostęp:
- Dostęp do wszystkich lekcji video
- Materiały do ćwiczeń
- Dodatkowe artykuły z trikami
- Formularze gotowe od razu do użycia
- E-booki pogłębiające Twoją wiedzę
- Certyfikat potwierdzający Twoje umiejętności
Masz już konto w serwisie?
Zaloguj się
 - Twój pierwszy krok do lepszych wyników
- Twój pierwszy krok do lepszych wyników



